Djikstra

Using the Dijkstra algorithm, it is possible to determine the shortest distance (or the least effort / lowest cost) between a start node and any other node in a graph. The idea of the algorithm is to continiously calculate the shortest distance beginning from a starting point, and to exclude longer distances when making an update.

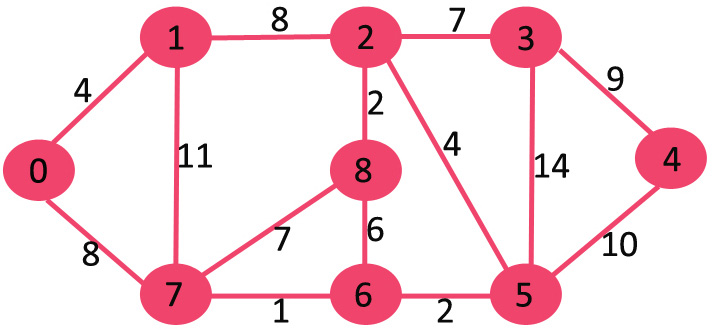
Key Points:

• Initialization of all nodes with distance "infinite".
• Initialization of the starting node with 0.
• There is a Queue named Q.

Pseudocode:

ShortestPath(G, v)
    init D array entries to infinity
    D[v]=0
    add all vertices to priority queue Q
    while Q not empty do
        u = Q.removeMin()
        for each neighbor, z, of u in Q do
            if D[u] + w(u,z) < D[z] then
            D[z] = D[u] + w(u,z)
        Change key of z in Q to D[z]
    return D as shortest path lengths

Result:

0 1 7 6 5 2 8 3 4

Complexity:

• To traverse all of the vertices, it leads to O(V^2).
• It can be reduced to O(E logV) with help of binary heap: http://www.geeksforgeeks.org/greedy-algorithms-set-7-dijkstras-algorithm-for-adjacency-list-representation/